Hoy la cosa va de números. ¿Quieres saber cuánto tiempo necesitas para duplicar el capital de tu cuenta? Para esto primero necesitamos revisar un poco algunos conceptos de matemática financiera básica : el interés compuesto, la media geométrica y la regla del 72.
Es bastante sencillo, así que busca tu calculadora o abre una hoja de cálculo que vamos a repasar algunos números…
El interés compuesto
El interés compuesto entra en juego cuando reinviertes tus beneficios (sumas las ganancia/pérdidas a tu capital inicial).
¿Por qué compuesto? Porque cada vez se suma la revalorización del año anterior y se vuelve a aplicar el interés. De esta forma los intereses producen cada vez más intereses generando un efecto bola de nieve.
Como ilustración, este ejemplo simple del interés compuesto puede ser útil:
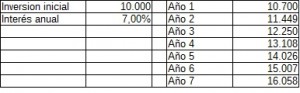
Inviertes 10.000€ a un tipo fijo de 7% anual.
El 7% de 10.000 son 700, entonces al final del primer año tendrás 10.700€. Pero al final del segundo no tendrás 11.400€ ( 10.700+700) sino que tendrás 11.449€. Esta diferencia de +49€ es fruto de haber reinvertido los beneficios.
¿Cuánto tiempo tomará duplicar el capital de tu cuenta?
Tomando el mismo ejemplo anterior. ¿En cuánto tiempo doblarías el dinero de tu cuenta?
El cálculo es sencillo si partimos de la fórmula de cálculo de interés compuesto.
Para calcular en cuántos años duplicas tu dinero invertido puedes tomar la opción fácil y reemplazar los números en un Excel.
Así puedes ver que a un 10% anual duplicarás tu capital en un poco más de 7 años.
Si la rentabilidad es del 4% anual serán casi 18 años para poder duplicar tu capital. Y si lo que obtienes es un 1% anual de rentabilidad (que es más o menos lo que pagan los depósitos bancarios en euros hoy en día), necesitarás aprox 70 años para poder duplicar tu capital. Vamos, que necesitas vivir muchos años para poder ver eso.
Si te interesa probarlo, al final del post puedes descargar la hoja de cálculo.
La fórmula del 7 o regla del 72
Si no quieres complicarte con formulas y cálculos en Excel hay un pequeño «truco» muy útil conocido como la «fórmula del 7» o «regla del 72«.
Es muy simple y se basa en dividir 72 entre el tipo de interés para saber aproximadamente cuántos años necesitas para poder duplicar tu dinero. Si hacemos la prueba repitiendo el ejemplo anterior: 72/10= 7,2 ; 72/4= 18; 72/1= 72. No son exactos pero si dan una aproximación.
Fácil, verdad? y sobretodo mucho más rápido cuando necesitamos calcular algo mentalmente. Hay una especie de leyenda en internet que dice que Warren Buffett utiliza la regla del 72 para calcular rápidamente que tan rentable es una inversión. No se si será cierto o si sólo es otro cuento sobre Buffett. Pero de todas maneras el truco del 72 es bastante útil.
♦ Recuerda que como en los casos anteriores aquí estamos hablando de un tipo de interés constante durante todo el periodo. En trading la tasa de rentabilidad no es constante y por lo tanto el cálculo no es tan sencillo de realizar. Estos solo son ejemplos de una manera fácil (que no exacta) de hacer aproximaciones.
La lógica de la regla del 7 la puedes encontrar jugando un poco con la fórmula del capital final. Si el capital final es el resultado del capital inicial multiplicado por 1 más el tipo de interés elevado al tiempo (número de años generalmente).
Si CF=CI*(1+R)^n
entonces duplicar el capital significa⇒ 2*CI=CI(1+R)^n
y a partir de allí 2=(1+R)^n ⇒ ln(2)=ln(1+R) ⇒n=(ln(2))/(ln(1+R)),
si sabemos que ln(2) es aproximadamente 0.7 entonces n=0.7/R
Si quieres saber más, en Internet he encontrado este vídeo «Cómo duplicar su dinero», donde se dan otros ejemplos sobre la regla del 72.
La media geométrica
Necesitas una esperanza matemática positiva para poder ganar a largo plazo con tu sistema de trading, esa siempre es la condición de base. Sin embargo, cuando reinviertes tus beneficios el importe de la ganancia final dependerá de la media geométrica.
Cómo calcular la media geométrica
Como puedes ver en la fórmula, la media geométrica en la raíz enésima de los productos de todos los términos.
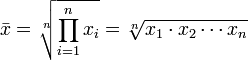
Si lo miras en un ejemplo será mucho más fácil:
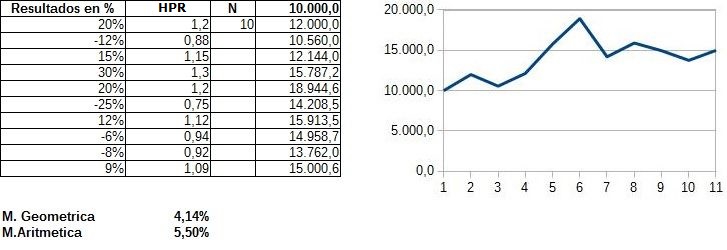
Partes de una inversión inicial de 10.000, y estos son los resultados de 10 operaciones:
+20%,-12%,+15% +30%,+20%,-25%,+12%,-6%,-8%,+9%.
A partir del resultado porcentual de las operaciones obtienes el HPR expresado como 1 +- el %
Así un incremento del 20% será 1,2 ( 1+0,2) y una pérdida de 12% será 0.88 ( 1-0,12).
Luego multiplicas los HPR y a su resultado le aplicas la raíz correspondiente al número de operaciones. En este caso 10, y por último restas 1.
La media geométrica es= 0.04138 ( 4.14%)
Si lo comprobamos como CF=CI(1+R)^n ⇒(10.0001.0413)^10= 15.000
La media geométrica se puede calcular también en Excel utilizando la función MEDIA.GEOM
Media geométrica vs media aritmética
- La media geométrica es siempre menor o igual que la media aritmética.
(En ejemplo anterior la media aritmética es del 5.5%). - La media geométrica es menos sensible que la media aritmética a los valores extremos
Para los que quieran jugar un poco con las fórmulas en este link dejo la hoja de cálculo para descargar: matematica financiera basica
Si te gustan los artículos recuerda que puedes suscribirte al blog y los recibirás directamente como newsletter en tu correo. Además lo puedes seguir / compartir por Facebook, Twitter, Feedly, etc.






Muy buena entrada. A veces es bueno sistematizar y pasar por el filtro de las matemáticas nuestros anhelos, jaja.
Un saludo y enhorabuena por el NIVEL.
Gracias a ti @tradingpulsar, por pasarte por el blog y comentar.
un saludo
en la formula CF=CI*(1+R)^n
que significa R y n?
Hola Maxi,
seria:
capital final = capital inicial multiplicado por (1 + tipo d interés) elevado al tiempo
En el artículo se hace mención a la hoja de cálculo: «matematica financiera basica»
que no he conseguido abrir. ¿Podríais ayudarme?
Hola Acróbata,
es un link que permite descargarte el archivo. Lo puedes abrir con Excel.
Dime si te funciona, si no te lo envío por mail.
Hola. Excelente información. El interés compuesto y la duplicación de capital, parecen rentables opciones para ahorrar dinero. Creo que la opción podría verse también como refugio de valor, frente a la inflación y otras perdidas de valor con el tiempo. Personalmente nunca he invertido en bolsa y desconozco el mecanismo de los pagos, comisiones y impuestos correspondientes. Entonces mi duda es la siguiente..
Si yo tengo exactamente 1000€ y decido invertirles en bolsa con un interés compuesto del 5% promedio anual, necesitaré 14,4 años para duplicarlos, eso me quedo claro. Como mi capital inicial es de 1000€ exactos, tengo que descontar todos los gastos que conlleva la inversión. Supongo que se pagan ciertas comisiones y gastos a la entrada de la inversión.. ¿Cuales son?. También supongo que se pagan ciertas comisiones y gastos a la retirada del dinero..¿Cuales son?. Deduzco que estos beneficios hay que declararles a hacienda para que puedan cobrarse la parte proporcional, etc.. Entones nos seria muy útil tener a mano una formula, que aun trabajando con números variables, pueda arrojarnos más luz sobre las verdaderas ganancias que producirían esos 1000€ despues de sacarles a los 14,4 años. Gracias.
Hola Dani,
Un punto importate a aclarar es que cuando inviertes en bolsa la tasa de rentabilidad no es constante y por lo tanto el cálculo no es tan sencillo( lineal) de realizar. En el caso del ejemplo ( como el de la regla del 72) estamos hablando de un tipo de interés constante durante todo el periodo.
Respecto a las comisiones e impuestos: depende.
Los impuesto dependerán de dónde es tu residencia fiscal y también de la evolución de las leyes tributarias. Por ejemplo, en España los últimos años han habido varias modificaciones sobre la tributación de los dividendes de un ejercicio al otro.
Respecto a las comisiones, también depende de con qué entidad realices tus inversiones. Parece que te estoy dando una respuesta demasiado aproximativa pero en el tema de comisiones te puedes encontrar desde operaciones a 1 USD por tramo hasta 30 USD por tramo. Depende de cuál sea tu broker y tus condiciones.
interesante el tema de la duplicación del capital utilizando la media geométrica, pues estoy haciendo un pequeño trabajo de investigación acerca de la anemia, no quiero utilizar modelos para los pronóstico porque los resultados son erróneos.
Excelente blog.
Gracias Federico
Gracias , muy buena info!
Me pueden enviar el link a mi correo de: Matematicas financiera basica, ya que no puedo abril el publicado
Qué tasa de interés bimestral me triplica una inversión en 4 años