
Cuando intentas meter mano a modelos de finanzas cuantitativas comienzan las dudas. Algunas de estas dudas pueden tener origen en algunos conceptos bastante básicos:
Por ejemplo, una de mis dudas es ¿por qué algunos modelos cuantitativos utilizan la rentabilidad logarítmica– o rendimientos compuestos contínuos- en vez de la rentabilidad simple?
¿Qué finalidad tiene calcular rendimientos logarítmicos en vez de los rendimientos simples?
Bueno, hasta ahora he encontrado estas posibles respuestas:
1) Problemas entre la rentabilidad simple y la distribución normal
Muchos de los modelos de evaluación del riesgo se basan en la distribución normal de las series de datos. Pero el problema es que este tipo de distribución puede no ser adecuada para representar la rentabilidad simple.
Para ilustrar por qué no es adecuada, voy a reproducir este ejemplo del curso «Introduction to Computational Finance and Financial Econometrics» de Coursera
Primero comenzamos por repasar rápidamente algunos conceptos:
La rentabilidad simple o aritmética es la variación porcentual del precio que utilizamos habitualmente y que todos conocemos:
Rentabilidad simple=(Precio inicial-precio final) / precio inicial
El rentabilidad logarítmica, o capitalización compuesta continua, se calcula usando logaritmos naturales:
Rc = ln (Precio inicial / Precio final)
Rc= ln (1+ Rentabilidad simple)
Recordando nuestras bases de estadística de la escuela, podemos aplicar los conceptos de media, varianza y desviación típica para evaluar la rentabilidad y el riesgo de las inversiones. Así, podemos interpretar la media de una serie de retornos como el retorno esperado y la desviación como la dispersión de los retornos.
Ahora el ejemplo:
Supongamos que tenemos una inversión anual en una acción de bolsa, simple sin apalancamiento. Asumimos que el retorno sigue una distribución normal con una media de 0.05 (5% de rentabilidad) y una desviación típica de 0.5 (50%)
Si lo vemos en un gráfico:
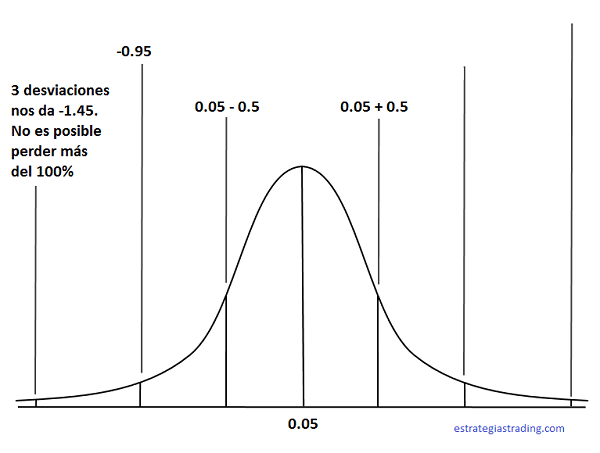
Podemos ver que la media de datos se sitúa en 0.05 y que la primera desviación estándar corresponde a 0.05+ 0.5=0.55 y 0.05 – 0.5=-0.45 (Valor medio + – una desviación estándar).
Es decir que según el ejemplo, con que la rentabilidad fuera inferior en 1 desviación estándar perderías -0.45, es decir el 45% de la inversión.
Si sobre el lado negativo nos movemos dos desviaciones, entonces tenemos que el resultado es 0.05 – (2*0.5)= -0.95 . Perderías el 95% del dinero.
¿Y qué pasa si nos movemos a 3 desviaciones? Pues 0.05 -(3*0.5)= -1.45 Nos da un resultado imposible ya que indica que estarías perdiendo más del 100% de tu inversión.
Si lo calculas, la distribución del ejemplo muestra que hay 1.8% de probabilidad de que el precio en el futuro sea negativo.
El problema viene porque la distribución normal está definida para todos los valores reales, lo que comprende rentabilidades entre -∞ y +∞. ¡Pero no podemos tener rentabilidades infinitas negativas! la mayor pérdida que en realidad puedes tener es el 100% de tu inversión ya que no puedes tener precios negativos.
Utilizar la rentabilidad logarítmica
¿Qué pasaría si utilizáramos la rentabilidad logarítmica – retorno compuesto contínuo- en vez de los retornos simples?
Si tomamos el mismo ejemplo de antes, pero en este caso asumimos que el retorno compuesto continuo es el que sigue una distribución normal (y seguimos utilizando una media de 0.05 y una desviación típica de 0.5 ).
¿Qué pasa cuando lleguemos a 3 desviaciones? Que la rentabilidad logarítmica sera de -1.45 (0.05- 3*0.5). ¿Y cuánto es esto en rentabilidad simple?
Veamos, si:
Rc= ln (1+ Rentabilidad simple) → Rentabilidad simple=e^Rc-1
Rentabilidad=(e^-1.45 )-1 = -0.765. Será igual a una pérdida del 76,5%.
No llega a dar la probabilidad de precios negativos.
Otros ejemplos:
- Un interés compuesto continuo de -2 nos da una rentabilidad simple de -0.865. Es decir si el interés compuesto continuo es de -200%, significa que habrás perdido el 86.5% de tu dinero.
- Si llegas a una rentabilidad logarítmica de -∞, tendrás una rentabilidad de -1 ( pérdida de 100%):
Rentabilidad=(e^-∞ )-1 = -1
( recuerda las propiedades de las funciones exponenciales e^-∞=0)
La rentabilidad logarítmica no puede ser menor a -1. Es por esto que se utilizan los rendimientos logarítmicos para calcular probabilidades basadas en la distribución normal.
2) Permite sumar rentabilidades en el tiempo
Cuando trabajas con rentabilidades simples, la relación entre los periodos es por multiplicación Por ejemplo, en una inversión anual la rentabilidad es la media geométrica de las rentabilidades mensuales.

El problema viene por esta relación de multiplicación, ya que el producto de variables normalmente distribuidas no es una variable normal. En cambio, la suma de las variables distribuidas normalmente si es normal. Por lo que es mejor utilizar la suma de rentabilidades que la multiplicación.
Con la rentabilidad logarítmica sí se puede sumar la rentabilidad de los distintos periodos para obtener la rentabilidad total.
Por lo que la rentabilidad compuesta de n periodos, no es más que la diferencia entre ln(precio final) – ln(precio inicial)
∑ ln(1+r) = ln(1+r1) + ln(1+r2)+…+ln(1+ rn) = ln(p.inicial) – ln(p.final)
Quizás otro sub-punto extra…
A nivel de cálculo, otra ventaja de utilizar los rendimientos logarítmicos es que si la rentabilidad logarítmica baja de 0.26 un día y sube de 0.26 al siguiente, la variación total es de 0. Esto no es así con la rentabilidad simple donde los porcentajes de ganancia y pérdidas no son simétricos. ( ver: cuánto cuesta recuperar una pérdida)
| Precio | Ren.Simple | Ren.Ln | |
| t0 | 130 | ||
| t1 | 100 | -0,23 | -0,26 |
| t2 | 130 | 0,30 | 0,26 |
3) Igualdad aproximada
Cuando la rentabilidad es muy pequeña, si pensamos en operaciones de trading a corto plazo ese suele ser el caso, los retornos logarítmicos son aproximadamente iguales a los retornos simples.
ln (1+r) ≈ r, r <<1
Si quieres ver más sobre el tema, aquí hay un post de Quantivity que lo explica bastante bien.
Si te gustan los artículos de esta web, recuerda que puedes suscribirte por correo electrónico y recibirás las entradas y los extras directamente en tu correo.
También puedes seguir a Estrategias de Trading por Twitter, Feedly o nuestra página de Facebook.



Buenas tardes Duk Dos:
En el artículo de arriba «3 Razones para utilizar la rentabilidad logarítmica» encuentro varias cosas que para mí no estan claras y me gustaría poder explicarme, lo que ocurre es que no sé cómo poner fórmulas sencillas en este apartado, quizá si pudiera «pegar» un escrito en formato word …
En fin, resumiré algo y agradecería que alguien me ayudara para poder formular comentarios más concretos.
Se tata de comparar retornos (entendidos, al parecer, como rendimientos de periodo unitario) expresados con escala lineal y logarítmica – de acuerdo con el «post Quantivity» adjunto en el artículo-. No creo que se trate de ninguna comparación entre intereses simples y compuestos.
La rentabilidad simple Rs = r=(Precio final – Precio inicial)/Precio inicial, de aquí:
Pf/Pi = 1+r y como la base e elevada a log.nepedePepito =Pepito (por def. de log. neperiano), resulta: e(elevado a Ln (Pf/Pi)) = 1+r, y también:
log (Pf/Pi) = log (1+r).
En la distribucion normal de la variable retornos X = N(0.05; 0.50), la probabilidad de que el retorno sea < 0,05 es, loógicamente, del 50%; pero empezarán a ser negativos (X<0) con el 41% de probabilidad, no del 1.8% (?).
Si utilizamos los logaritmos de unos valores, sus verdaderos valores se obtendrán con el antilog, de no ser que directamente nos lo dé una escala gráfica, por ejemplo.
Quizá trabajando con un una serie de retornos a modo de ejemplo se podría ver más claro.
Saludos
Acróbata
19/01/2017
Creo que hay una errata, donde pone «La rentabilidad logarítmica puede ser menor a -1» debería referirse a la rentabilidad simple, No? O poner que la rentabilidad logaritmica no puede ser menor a -1
Hola Andrés. Si había una errata, ya la he corregido. Gracias por avisar.
saludos,
Yo veo la misma errata que acróbata.
La expresiones de rentabilidades creo que están al revés.
Aumentos de capital saldrían rentabilidades negativas.
De hecho ejemplo de cálculo de la tabla sale bien pero con el cálculo al revés.
Amigo, creo que el calculo es un poco raro de la rentabilidad cundo colocas precio inicial / precio final, si el precio final el mayor te da negativo el ln(precio inicial / precio final).
Creo que no esta bien el orden de los factores.
@Willy wonka
ln (1 +( (Pi-Pf)/Pi))
ln ((Pf+Pi-Pf)/Pi)
ln (Pi/Pf)